Some notes on mixtures of normal distributions
There is not much use in belaboring about the importance of normal distributions - they are ubiquitous, versatile and have tremendous utility in sampling statistics (thanks to Central Limit Theorem). In this post, however, we aim to answer the following questions - what happens when two normal distributions are combined? And more interestingly, when does the mixture of two normal distributions end up being bimodal? Mixtures of normal (Gaussian) distributions are especially important in high dimensional clustering problems. There have been some thorough investigations on this topic (see for instance, Is Human Height Bimodal?), but actual implementations of this transition from a unimodal to a bimodal distribution have been lacking. Hence, the current post.
Preliminaries
When two normal distributions are combined under mundane conditions (read when the two means are not too far apart from each other), the resulting mixture distribution tends to be a normal distribution as well. The properties of the said mixture distribution will be as follows -
\( \mu_{mix} = \mu_1 + \mu_2 \)
\( \sigma_{mix} = \sqrt{\sigma_1^2 + \sigma_2^2} \)
The \( \mu \) and \( \sigma \) correspond to mean and standard deviation, respectively. Note that the standard deviation of the mixture takes the above form because the variances get added.
This generalizes to \( n \) distributions as follows:
\( \mu_{mix} = \sum_{i=1}^{n} \mu_i \)
\( \sigma_{mix} = \sqrt{\sum_{i=1}^{n} \sigma_i^2} \)
There are some interesting implications that follow from the above expressions. Consider the following example -
Given a normally distributed r.v. A with \( \mu=10 \) and \( \sigma=1 \), sample 100 values from the distribution and store in a variable X. Assign Y = sum (X [idx]), where idx is the odd indices. What is the variance of Y?
Since we are adding 50 values, each of which can be considered to have the same distribution as the original r.v. A, the problem reduces to finding the variance of the summation of 50 normally distributed r.v.’s. From the above expression, this would turn out to be \( \sigma_{mix}=\sqrt{50} \).
Another example -
Consider two normal distributions - X ~ \( N(3,5^2) \) and Y ~ \( N(2,5^2) \). What is the mean and variance of Z = 2X - Y?
The important point to note here is that when a distribution is multiplied by a scalar, the mean and variance also get multiplied by the scalar.
So, \( \mu_Z = 2 \times \mu_X - \mu_Y = 2 \times 3 - 2 = 4 \)
And, \( Var (Z) = Var (2X) + Var (-Y) = 2^2 \times Var(X) + Var(Y) = 4(5^2) + 5^2 = 125 \).
When does a mixture distribution become bimodal?
It is not my interest here to prove when a mixture distribution becomes bimodal - that has already been done in prior literature (see refs [1] and [2] below). Instead, we are interested in performing a quick visualization of the mixture distribution resulting from combining two normal distributions. We will take some sample data and write some code.
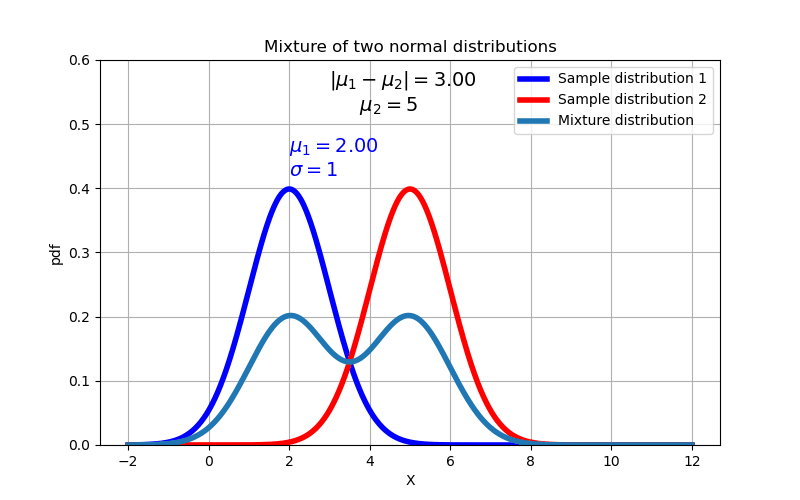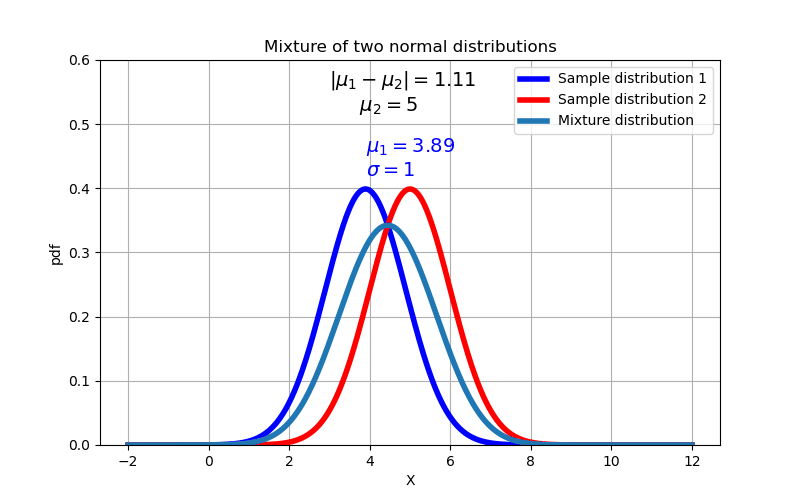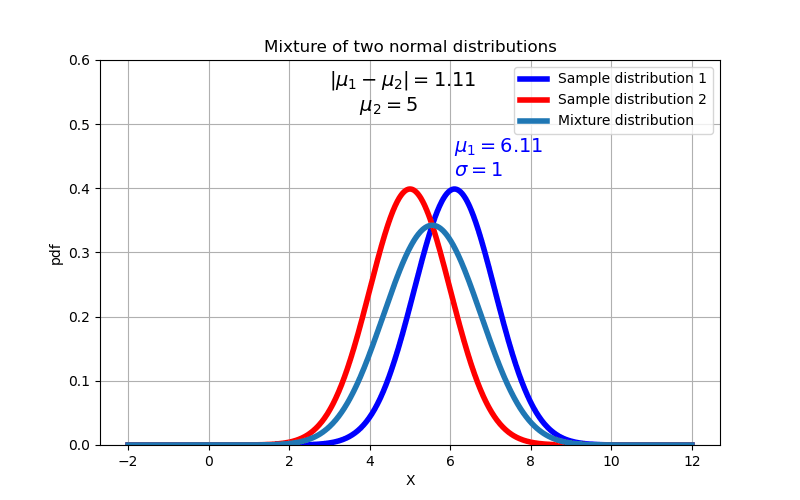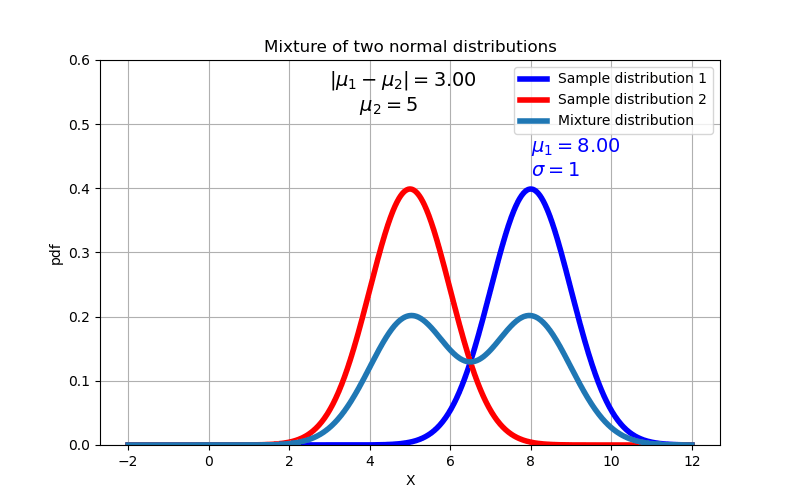
As expected, we find that the mixture distribution transitions from a unimodal distribution to a bimodal distribution when the difference between the means exceeds 2 times the standard deviation.
So, is human height bimodally distributed?
We return to the earlier question about human heights - is it really bimodally distributed? We have access to some reliable data on population heights. (This data was also investigated in an earlier post.)
The mean and standard deviations of heights of men and women are the following:
\( \mu_{women} \) = 163 cm
\( \mu_{men} \) = 178 cm
\( \sigma_{women} \) = 7.3 cm
\( \sigma_{men} \) = 7.7 cm
We adopt the same procedure as above and compute the mixture distribution of the two normal distributions to obtain the following -
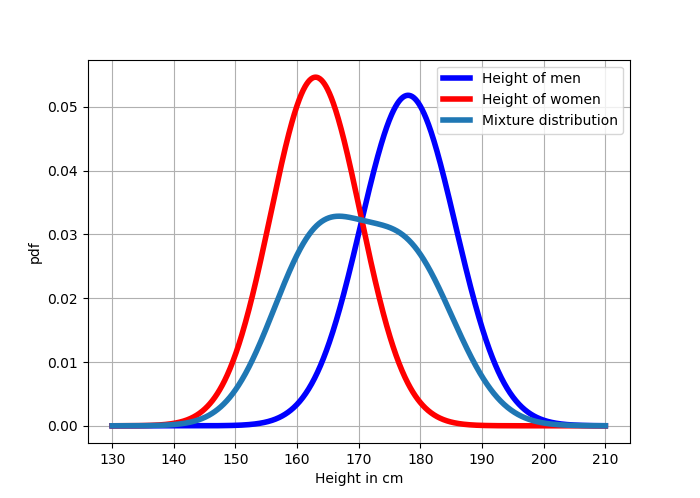
The code to generate the above plot is given below for completeness:
From the above plot, the mixture distribution is clearly not a bimodal distribution. So, at least for the current set of data that we used, human height is not bimodal.