Importance Sampling
Importance Sampling is a method of approximating the properties of a particular distribution which forms a subset of Monte Carlo methods. Importance Sampling is not a sampling technique as the name would suggest, but instead is a variation reduction technique where we are typically working with distributions that are difficult to sample from. Hence we estimate the properties of the said distribution using an alternative distribution whose properties are more conducive for the problem at hand. In other words, there are usually certain values of a distribution that are more critical to parameter estimation than others, and importance sampling involves choosing a distribution which emphasizes the important values. An unbiased estimate is formed by multiplying the original estimate by an appropriate likelihood ratio. In this post, we will cover the basics of importance sampling and when it becomes useful. We will also consider a couple of toy problems.
\( E(X) = \int f(x) p(x) dx \)
where \( p(x) \) is the pdf of \( f(x) \).
\( E(X) = \int f(x) \frac{p(x)}{q(x)} q(x) dx \)
Here, \( \frac{p(x)}{q(x)} \) is the likelihood ratio. This simplifies to the following expression:
\( E(X) = E_q [\frac{p(x)}{q(x)}] \)
Example 1 - Calculating the expected value of a biased die
For our first example, we will consider two dice - a fair die and a biased die. The initial probability density functions for the two dice are shown in the figures below. The goal is to estimate the expected value of the biased die by sampling values only from the fair die distribution.
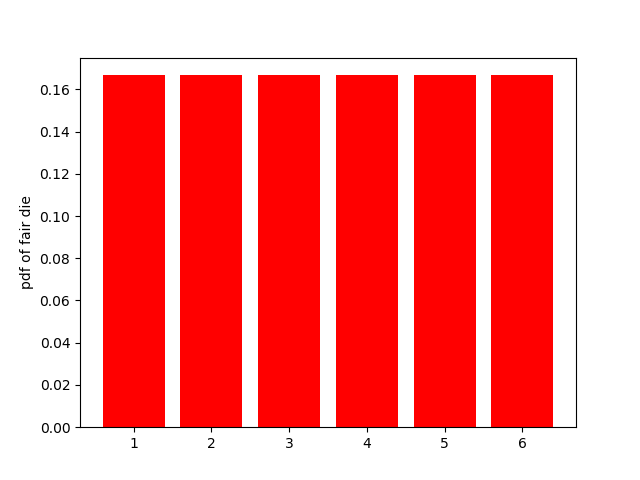
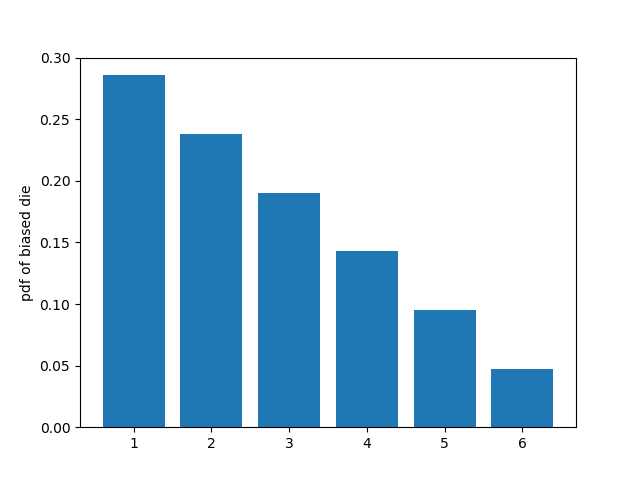
The Monte Carlo simulation using importance sampling is coded below:
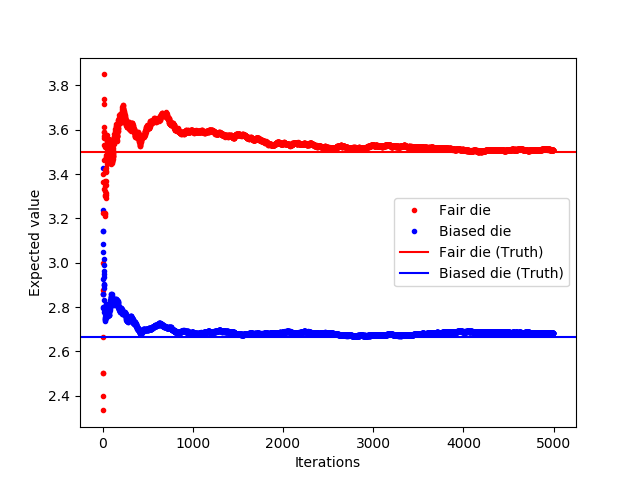
Note that in the above code, we are only sampling values from the fair die distribution and multiplying the result with the likelihood ratio. The resulting figure shows the convergence of the expected values. Also note that in the above toy example, the variance reduction property of importance sampling is not observed; here, Monte Carlo in its conventional form and importance sampling both have the same variance. The purpose was to provide a template of implementation of importance sampling for other cases where the variance reduction aspect would be more evident.
Example 2 - Estimating the prevalence of rare events
When simulating the prevalence of rare events (i.e., events for which the probability of occurrence is very small), conventional Monte Carlo simulations can take a really long time before a single occurrence of the event is realized. Importance sampling can be used instead where the sampling distribution is chosen such that we sample more often in the domain of the said rare event. We will again consider an example to illustrate this concept. The following example was inspired by Prof. Tom Kennedy’s lecture notes.
We will start by defining \( Z \) to be a standard normal distribution (\( N(0,1) \)). We would like to compute a quantity with a low probability, say, \( P(Z \geq 4) \). As mentioned above, using the typical Monte Carlo simulation to perform this would be futile as there won’t be many samples generated in the domain \( Z \geq 4 \) (probably zero). As a result, the associated variance is very large. Instead, we use an alternative sampling distribution.
For \( N(0,1) \), \( p(x) = \frac{1}{\sqrt{2\pi}}\exp(-x^2/2) \).
We will take the sampling distribution to be \( q(x)=\exp(-(x-4)) \), for \( x \geq 4 \).
Now, we will just sample values for \( x \geq 4 \), and compute the required probability using the appropriate likelihood ratio:
\( p=\int p(x)dx \)
\( p=\int \frac{p(x)}{q(x)} q(x) dx \)
and the likelihood ratio is
\( w=\frac{p(x)}{q(x)}=\frac{1}{\sqrt{2\pi}}\exp(-x^2/2+x-4) \)
The simulation to perform these calculations is rather straightforward as shown in the code below:
The estimated probability of \( (Z \geq 4) \) = 3.324e-07
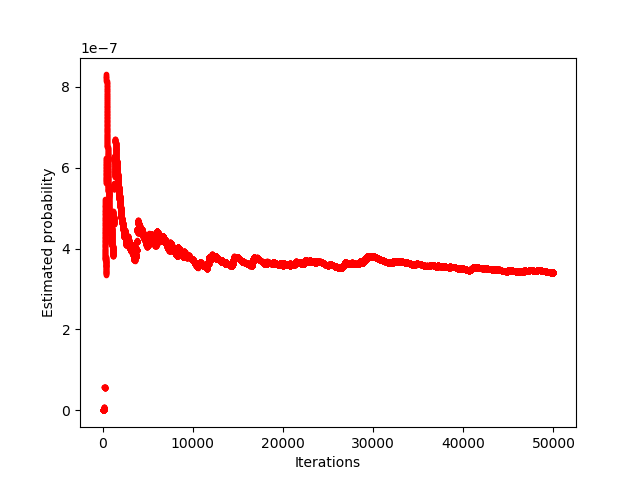
The above figure shows the convergence of the probability after a fairly large number of iterations. Note that given the low estimated probability, it is very likely that we would not have realized a single instance of this event using conventional Monte Carlo methods.
The variance from importance sampling is no greater than \( \exp(-8)/\sqrt{2\pi} \) squared or \( \exp(-16)/\sqrt{2\pi} \). The original variance of conventional Monte Carlo was of the order of \( \exp(-8) \). There is a significant reduction in the variance as a result of using importance sampling in this problem.